变分贝叶斯推断

问题描述

假设当前有一个贝叶斯模型，且其中的参数都有相应的先验分布。同时，模型中还可能有潜变量，将其与各种参数标记为$\Theta$。同样地，把所有观测变量集合标记为$\mathcal{Y}$。因此，我们希望找到分布$q(\Theta)$来逼近真实后验分布$p(\Theta\mid\mathcal{Y})$，而这可以通过最小化KL散度实现，也即：

$$\begin{equation} \begin{split} \text{KL}(q(\Theta)\|p(\Theta|\mathcal{Y}))&=\int q(\Theta)\text{ln}\left\{\frac{q(\Theta)}{p(\Theta\mid\mathcal{Y})}\right\}d\Theta \\ &=\text{ln}p(\mathcal{Y})-\int q(\Theta)\text{ln}\left\{\frac{p(\mathcal{Y},\Theta)}{q(\Theta)}\right\}d\Theta \end{split} \end{equation}$$

其中$\text{ln}p(\mathcal{Y})$表示模型证据（Evidence），则其下界（lower bound）可以定义为$\mathcal{L}(q)=\int q(\Theta)\text{ln}{\frac{p(\mathcal{Y},\Theta)}{q(\Theta)}}d\Theta$。因为模型证据是一个常量，当KL散度为0时，下界出现最大值，这就意味着$q(\Theta)=p(\mathcal{Y},\Theta)$。

平均场理论

根据平均场理论（mean field theory），我们假设变分分布$q(\Theta)$可以被分解成各组变量分布的乘积，即可以写作：

$$\begin{equation} q(\Theta)=\prod_{j}^{M}q_j(\Theta_j) \end{equation}$$

这是针对该分布的唯一假设，其中每一个独立因子$q_j(\Theta_j)$的特定函数形式可以具体地一个个推导出来。通过最大化下届$\mathcal{L}(q)$，第$j$个因子的优化形式由下式给出：

$$\begin{equation} \text{ln}q_j(\Theta_j)=\mathbb{E}_{q(\Theta\backslash\Theta_j)}\left[\text{ln}p(\mathcal{Y},\Theta)\right]+\text{const} \end{equation}$$

其中$\mathbb{E}_{q(\Theta\backslash\Theta_j)}\left[\cdot\right]$表示关于除$\Theta_j$外所有变量的$q$分布的期望。因为所有参数的分布都属于指数族分布，且都与其父节点共轭，因此我们能够通过公式(3)推导出$\Theta$中每个参数的后验分布更新的近似形式。

变分下界

在模型计算时，可以通过直接计算变分下界$\mathcal{L}(q)$来判断算法是否收敛，因为在每一次迭代中变分下界不减。变分下界可以通过下式进行计算

$$\begin{equation} \begin{split} \mathcal{L}(q)&=\int q(\Theta)\text{ln}\left\{\frac{p(\mathcal{Y},\Theta)}{p(\Theta)}\right\}d\Theta \\ &=\mathbb{E}_{q}[\text{ln}p(\mathcal{Y},\Theta)]-\mathbb{E}_{q}[\text{ln}q(\Theta)] \\ &=\mathbb{E}_{q}[\text{ln}p(\mathcal{Y}\mid\Theta)]+\mathbb{E}_{q}[\text{ln}p(\Theta)]-\sum_{j}\mathbb{E}_{q_j(\Theta_j)}[\text{ln}q_j(\Theta_j)] \end{split} \end{equation}$$

其中第一项表示联合分布的后验期望，而第二项则表示后验$q$分布的熵$H(q(\Theta))=-\mathbb{E}_{q}[\text{ln}p(q(\Theta))]$。

例子-一元高斯模型

模型推断

给定一组观测数据值$\mathcal{D}={x_1,x_2,\dots,x_N}$，假定数据是独立地从高斯分布中抽取的，目标是通过最大化后验分布推断得到均值参数$\mu$和精度参数$\tau$，其似然函数为

$$\begin{equation} \begin{split} p(\mathcal{D}\mid \mu,\tau)&=\prod_{i=1}^{N}\left(\frac{\tau}{2\pi}\right)^{\frac{1}{2}}\text{exp}\left\{-\frac{\tau(x_i-\mu)^2}{2}\right\} \\ &=\left(\frac{\tau}{2\pi}\right)^{\frac{N}{2}}\text{exp}\left\{-\frac{\tau}{2}\sum_{i=1}^{N}(x_i-\mu)^2\right\} \end{split} \end{equation}$$

同时引入参数$\mu$和$\tau$的共轭先验分布，其形式为

$$\begin{equation} \begin{split} p(\mu\mid\tau)&= \mathcal{N}(\mu\mid\mu_{0},\left[\lambda_{0}\tau\right]^{-1})\\ p(\tau)&= \text{Gam}(\tau\mid a_0,b_0) \end{split} \end{equation}$$

则其联合分布可以表示为

$$\begin{equation} \begin{split} p(\mathcal{D},\mu,\tau)=p(\mathcal{D}\mid\mu,\tau)p(\mu\mid\tau)p(\tau) \end{split} \end{equation}$$

对后验概率分布的变分近似进行分解

$$\begin{equation} q(\mu,\tau)=q_{\mu}(\mu)q_{\tau}(\tau) \end{equation}$$

根据公式(3)，可以推导出各个因子的优化形式，对于$q_{\mu}(\mu)$，我们有

$$\begin{equation} \begin{split} \text{ln}q_{\mu}^{*}(\mu)&=\mathbb{E}_{\tau}[\text{ln}p(\mathcal{D}\mid\mu,\tau)+\text{ln}p(\mu\mid\tau)]+\text{const} \\ &=-\frac{\mathbb{E}[\tau]}{2}\left\{\sum_{i=1}^{N}(x_i-\mu)^2+\lambda_0(\mu-\mu_0)^2\right\}+\text{const} \\ &=-\frac{1}{2}\left\{(\lambda_0+N)\mathbb{E}[\tau]\mu^2-2(\lambda_0\mu_0+N\bar{x})\mathbb{E}[\tau]\mu\right\}+\text{const} \end{split} \end{equation}$$

由共轭性，可以看到$q_{\mu}(\mu)$是一个高斯分布，其参数为

$$\begin{equation} \begin{split} \lambda^{*}&=(\lambda_0+N)\mathbb{E}[\tau] \\ \mu^{*}&=[\lambda^*]^{-1}(\lambda_0\mu_0+N\bar{x})\mathbb{E}[\tau] =\frac{\lambda_0\mu_0+N\bar{x}}{\lambda_0+N} \end{split} \end{equation}$$

同理，因子$q_{\tau}(\tau)$的最优形式为

$$\begin{equation} \begin{split} \text{ln}q_{\tau}^{*}(\tau)&=\mathbb{E}_{\mu}[\text{ln}p(\mathcal{D}\mid\mu,\tau)+\text{ln}p(\mu\mid\tau)+\text{ln}p(\tau)]+\text{const} \\ &=(a_0-1+\frac{N+1}{2})\text{ln}\tau-\left\{b_0+\frac{1}{2}\mathbb{E}\mu\left[\sum_{i=1}^{N}(x_i-\mu)^2+\lambda_0(\mu-\mu_0)^2\right]\right\}\tau+\text{const} \end{split} \end{equation}$$

因此$q_{\tau}(\tau)$是一个Gamma分布，参数为

$$\begin{equation} \begin{split} a^{*}&=a_0+\frac{N+1}{2} \\ b^{*}&=b_0+\frac{1}{2}\mathbb{E}\mu\left[\sum_{i=1}^{N}(x_i-\mu)^2+\lambda_0(\mu-\mu_0)^2\right] \end{split} \end{equation}$$

为了评估模型的收敛性，我们进一步计算变分下界，其公式如下

$$\begin{equation} \begin{split} \mathcal{L}(q)&=\mathbb{E}_{q}[\text{ln}p(\mathcal{Y},\Theta)]-\mathbb{E}_{q}[\text{ln}q(\Theta)] \\ &=\mathbb{E}_{q(\mu,\tau)}[\text{ln}p(\mathcal{D}\mid\mu,\tau)]+\mathbb{E}_{q(\mu,\tau)}[\text{ln}p(\mu\mid\tau)]+\mathbb{E}_{q(\tau)}[\text{ln}p(\tau)]-\mathbb{E}_{q(\mu)}[\text{ln}q(\mu)]-\mathbb{E}_{q(\tau)}[\text{ln}q(\tau)] \end{split} \end{equation}$$

上式各个部分可以通过下面公式计算得到，其中$\mathbb{E}q[\mu^2]=\mathbb{E}{\mu}[\mu^2]=(\mathbb{E}[\mu])^2+\text{Var}[\mu]$，$\mathbb{E}q[\text{ln}\tau]=\mathbb{E}{\tau}[\text{ln}\tau]=\psi(a)-\text{ln}b$，$\psi(\cdot)$为双伽马函数（digamma function）而$\Gamma(\cdot)$为伽马函数。

$$\begin{equation} \begin{split} \mathbb{E}_{q}[\text{ln}p(\mathcal{D}\mid\mu,\tau)]&=-\frac{N}{2}\text{ln}(2\pi)+\frac{N}{2}\mathbb{E}_q[\text{ln}\tau]-\frac{1}{2}\mathbb{E}_q[\tau]\mathbb{E}_q[\sum_{i=1}^{N}(x_i-\mu)^2] \\ &=-\frac{N}{2}\text{ln}(2\pi)+\frac{N}{2}(\psi(a^*)-\text{ln}(b^*))-\frac{a^*}{2b^*}\left\{\sum_{i=1}^{N}x_i^2-2\mu^*\sum_{i=1}^{N}x_i+\mathbb{E}_q[\mu^2]\right\} \\ \end{split} \end{equation}$$ $$\begin{equation} \begin{split} \mathbb{E}_{q}[\text{ln}p(\mu\mid\tau)]&=-\frac{1}{2}\text{ln}(2\pi)+\frac{1}{2}\mathbb{E}_q[\text{ln}(\lambda_0\tau)]-\frac{\lambda_0}{2}\mathbb{E}_q[\tau]\mathbb{E}_q[(\mu-\mu_0)^2] \\ &=-\frac{1}{2}\text{ln}(2\pi)+\frac{\text{ln}\lambda_0}{2}+\frac{1}{2}(\psi(a^*)-\text{ln}(b^*))-\frac{\lambda_0 a^*}{2b^*}\left\{\mathbb{E}_q[\mu^2]-2\mu_0\mu^*+\mu_0^2\right\} \\ \end{split} \end{equation}$$ $$\begin{equation} \begin{split} \mathbb{E}_{q}[\text{ln}p(\tau)]&=-\text{ln}\Gamma(a_0)+a_0\text{ln}b_0+(a_0-1)\mathbb{E}_q[\text{ln}\tau]-b_0\mathbb{E}_q[\tau] \\ &=-\text{ln}\Gamma(a_0)+a_0\text{ln}b_0+(a_0-1)(\psi(a^*)-\text{ln}b^*)-b_0\frac{a^*}{b^*} \end{split} \end{equation}$$ $$\begin{equation} \begin{split} -\mathbb{E}_{q}[\text{ln}q(\mu)]&=\frac{1}{2}\text{ln}(2\pi)-\frac{\text{ln}\lambda^*}{2}+\frac{\lambda^*}{2}\left\{\mathbb{E}_q[\mu^2]-2(\mu^*)^2+(\mu^*)^2\right\} \\ &=\frac{1}{2}\text{ln}(2\pi)-\frac{\text{ln}\lambda^*}{2}+\frac{1}{2} \end{split} \end{equation}$$ $$\begin{equation} \begin{split} -\mathbb{E}_{q}[\text{ln}q(\tau)]&=\text{ln}\Gamma(a^*)-(a^*-1)\psi(a^*)-\text{ln}b^*+a^* \end{split} \end{equation}$$

至此，我们得到了关于参数$\mu$与$\tau$最优分布的表达式，且各自依赖于另一个分布的计算所得的一阶矩或二阶矩。因此通过初始化参数的值，可以通过不断迭代计算出后验分布。

在此例子中，由于模型简单且参数数量只有两个，因此我们可以通过直接求解上式的因子找到显示解。首先我们可以通过设置无信息先验（noninformative prior）来简化上述表达式，也即$\mu_0=\lambda_0=a_0=b_0=0$。根据Gamma分布的均值计算公式，我们有

$$\begin{equation} \begin{split} \frac{1}{\mathbb{E}[\tau]}=\frac{b^*}{a^*}=\mathbb{E}\left[\frac{1}{N+1}\sum_{i=1}^{N}(x_i-\mu)^2\right]=\frac{N}{N+1}(\overline{x^{2}}-2\bar{x}\mathbb{E}[\mu]+\mathbb{E}[\mu^2]) \end{split} \end{equation}$$

由公式(10)，我们可以获得近似分布$q_\mu(\mu)$的一阶矩与二阶矩

$$\begin{equation} \begin{split} \mathbb{E}[\mu]=\bar{x}, \mathbb{E}[\mu^2]=\bar{x}^2+\frac{1}{N\mathbb{E}[\tau]} \end{split} \end{equation}$$

将其代入公式(19)，可以解出$\mathbb{E}[\tau]$

$$\begin{equation} \frac{1}{\mathbb{E}[\tau]}=\overline{x^2}-\bar{x}^2 \end{equation}=\frac{1}{N}\sum_{i=1}^{N}(x_i-\bar{x})^2$$

代码示例

上节一元高斯的求解MATLAB代码如下所示，首先通过随机数生成器生成$N$个高斯分布的随机数作为模型观测值

clear;
% 生成高斯分布随机数
mu_real = 1;
tau_real = 1.5;
N = 200;
D = normrnd(mu_real, sqrt(1./tau_real), [N,1]);
sumD = sum(D);
sumD2 = sum(D.^2);

mu_est = mean(D); % 公式(20)
tau_est = 1./(mean(D.^2)-mean(D).^2); % 公式(21)
% 查看该一元高斯的分布图像
x_real=-4+mu_real:0.1:mu_real+4;
y_real=normpdf(x_real,mu_real,sqrt(1./tau_real));
x_est=-4+mu_est:0.1:mu_est+4;
y_est=normpdf(x_est,mu_est,sqrt(1./tau_est));
figure;plot(x_real,y_real,'-r.',x_est,y_est,'--b.');grid;

初始化模型参数和超参数

% 初始化参数和超参数
mu0 = 1e-6; % 无信息先验
lambda0 = 1e-6; % 无信息先验
a0 = 1e-6; % 无信息先验
b0 = 1e-6; % 无信息先验
mu = randn();
mus(1) = mu;
tau = rand();
taus(1) = tau;

LB = 0; % 变分下界
tol = 1e-5; % 收敛允许误差
maxiters = 100; % 迭代最大次数

可视化求解过程，将分别绘出模型参数的真值与估计值比较图、变分下界变化图和精度参数$\tau$的后验分布变化图

% 可视化求解过程
scrnsz = get(0,'ScreenSize');
h = figure('Position',[scrnsz(3)*0.25 scrnsz(4)*0.25 scrnsz(3)*0.5 scrnsz(4)*0.5]);
set(0,'CurrentFigure',h);
subplot(2,2,1); plot(mu_real, '-r.','LineWidth',1.5,'MarkerSize',10 ); title('Model parameter \mu'); xlabel('Iteration'); grid on;
subplot(2,2,2); plot(tau_real, '-r.','LineWidth',1.5,'MarkerSize',10 ); title('Model parameter \tau'); xlabel('Iteration'); grid on;
subplot(2,2,3); plot(LB, '-r.','LineWidth',1.5,'MarkerSize',10 ); title('Lower bound'); xlabel('Iteration'); grid on;
subplot(2,2,4); plot(0:0.1:20, gampdf(0:0.1:20, a0, 1./b0), 'r-'); title('Posterior pdf'); xlabel('Noise precision \tau'); grid on;
set(findall(h,'type','text'),'fontSize',12);
drawnow;

模型迭代求解

% 模型求解
for it=1:maxiters
    % 更新参数 mu，公式(10)
    lambda_new = (lambda0+N)*tau;
    mu_new = (1./lambda_new)*(lambda0*mu0+sumD)*tau;
    mu = mu_new;
    mus(it+1) = mu;
    E_mu2 = mu_new^2+1./lambda_new; % E[mu^2]=E[mu]^2+Var[mu]
    
    % 更新参数 tau，公式(12)
    a_new = a0+(N+1)./2;
    b_new = b0+0.5*(sumD2-2*(sumD+lambda0*mu0)*mu+(N+lambda0)*E_mu2+lambda0*(mu0^2));
    tau = a_new./b_new;
    taus(it+1) = tau;
    E_lntau = psi(a_new)-safelog(b_new); % E[ln(tau)]=psi(a)-ln(b)
    
    % 评估变分下界，公式(13)
    E_pD = -0.5*N*safelog(2*pi)+0.5*N*E_lntau-0.5*tau*(sumD2-2*mu*sumD+E_mu2);
    E_pmu = -0.5*safelog(2*pi)+0.5*E_lntau+0.5*safelog(lambda0)-0.5*lambda0*tau*(E_mu2-2*mu0*mu+mu0^2);
    E_ptau = -safelog(gamma(a0))+a0*safelog(b0)+(a0-1)*E_lntau-b0*tau;
    E_qmu = 0.5*safelog(2*pi)-0.5*safelog(lambda_new)+0.5;
    E_qtau = safelog(gamma(a_new))-(a_new-1)*psi(a_new)-safelog(b_new)+a_new;
    LB(it) = E_pD + E_pmu + E_ptau + E_qmu + E_qtau;
    
    % 可视化求解过程
    set(0,'CurrentFigure',h);
    subplot(2,2,1); plot(mu_real*ones(1,it+1), '-r.','LineWidth',1.5,'MarkerSize',10);hold on;plot(mu_est*ones(1,it+1), '--r.','LineWidth',1.5,'MarkerSize',10 );hold on;plot(mus, '-b.','LineWidth',1.5,'MarkerSize',10);hold off; title('Model parameter \mu'); xlabel('Iteration'); grid on;
    subplot(2,2,2); plot(tau_real*ones(1,it+1), '-r.','LineWidth',1.5,'MarkerSize',10);hold on;plot(tau_est*ones(1,it+1), '--r.','LineWidth',1.5,'MarkerSize',10 );hold on;plot(taus, '-b.','LineWidth',1.5,'MarkerSize',10);hold off; title('Model parameter \tau'); xlabel('Iteration'); grid on;
    subplot(2,2,3); plot(LB, '-r.','LineWidth',1.5,'MarkerSize',10); title('Lower bound'); xlabel('Iteration'); grid on;
    subplot(2,2,4); plot(0:0.05:2*tau, gampdf(0:0.05:2*tau, a_new, 1./b_new), '-r.', 'LineWidth',1.5); title('Posterior pdf'); xlabel('Noise precision \tau'); grid on;
    set(findall(h,'type','text'),'fontSize',12);
    drawnow;
    
    % 判断模型是否收敛
    if it>3
        LB_change = -1*(LB(it) - LB(it-1))/LB(3);
    else
        LB_change = NaN;
    end
    if it>10 && (abs(LB_change) < tol)
        disp('Converged!');
        break;
    end
end

function y = safelog(x)
x(x<1e-300)=1e-200;
x(x>1e300)=1e300;
y=log(x);
end

求解结果如下图所示，左上与右上两图中的红色实线表示生成观测数据模型参数的真值，红色虚线表示利用观测数据显式计算得到的模型参数的估计值，蓝色实线表示利用变分推断迭代求解的参数估计值。在本例子中，由于推断公式较简单，$\mathbb{E}[\mu]$的计算不依赖于$\mathbb{E}[\tau]$，所以算法在第二次迭代就已经收敛到显式计算的估计值。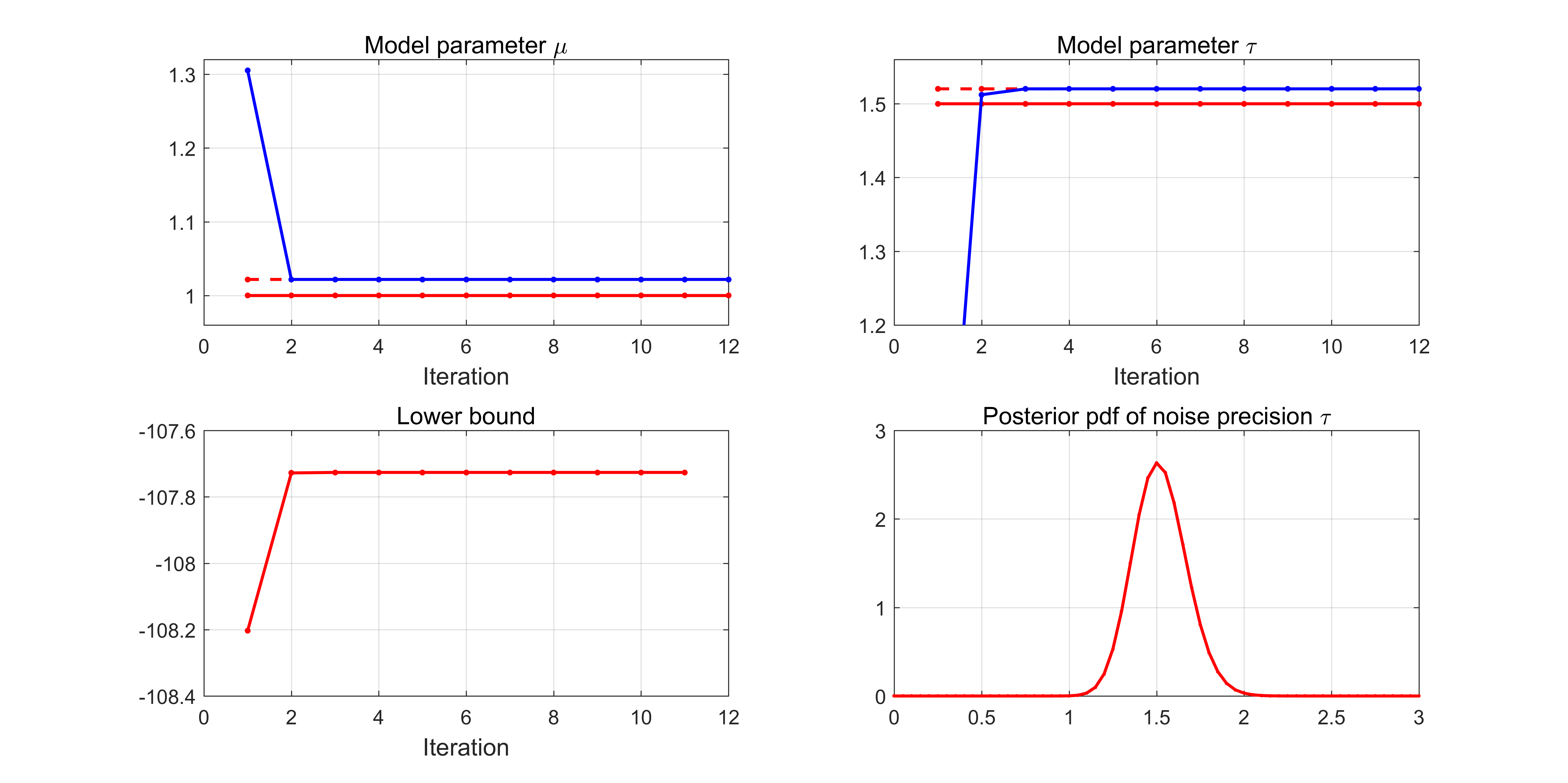

例子-混合高斯模型

模型推断

代码示例

参考

1. Christopher M. Bishop. “Pattern recognition and machine learning.” Springer, 2006.
2. PRML Errata 1st: https://www.microsoft.com/en-us/research/wp-content/uploads/2016/05/prml-errata-1st-20110921.pdf
3. Qibin Zhao, Liqing Zhang, and Andrzej Cichocki. “Bayesian CP factorization of incomplete tensors with automatic rank determination.” IEEE transactions on pattern analysis and machine intelligence, 2015.
4. https://github.com/qbzhao/BCPF
5. https://en.wikipedia.org/wiki/Gamma_distribution
6. https://en.wikipedia.org/wiki/Conjugate_prior