RDD（Resilient Distributed Dataset）译作弹性分布式数据集，是Spark中最常用的数据抽象，是一个只可读、可分区、可并行计算的数据集合。RDD允许将工作集缓存在内存中进行复用，大大地提升了查询速度。

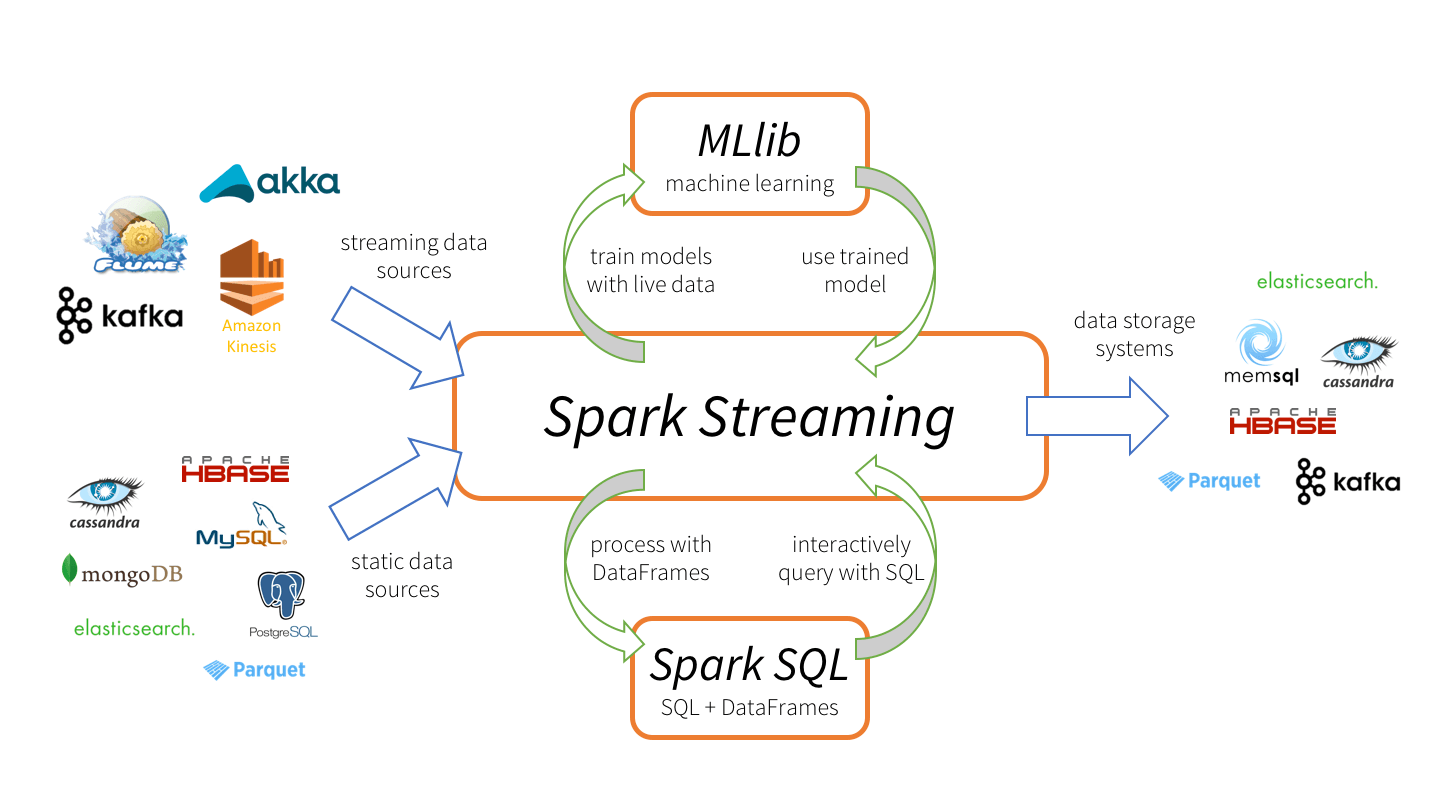
为了在有限的资源上学习大数据处理与分析技术，借鉴Linux以及部分网上的教程，在Windows10平台搭建Spark环境。本文将简单记录搭建流程以及其中遇到的坑。

本文记录本人使用Windows的必备软件工具，以及在使用中的设置习惯。

由于某些原因，国内访问ShareLaTeX或Overleaf网站速度特别慢而且经常掉线，科研环境十分不友好，因此有了自己搭建ShareLaTeX服务打算，且其支持Docker容器化部署，安装过程比较容易。本文记录了在实验室内网环境下利用Docker搭建ShareLaTeX服务的过程，并进行中文环境配置。

本地GitLab的安装需要部署各种依赖和其他服务，费时且麻烦，而直接使用Docker进行容器化部署则省时简单，只要运行一行命令即可使用。本文记录了在实验室内网环境下利用Docker搭建源码托管工具GitLab，并列出一些必要的个性化配置项。

贝叶斯泊松分解

一般形式

因为可以对观测数据进行灵活的符合实际的建模（不同的概率分布假设），贝叶斯概率分解模型已经成为了最常见的矩阵/张量分解方法。其中，贝叶斯泊松分解模型一方面可以对计数值（count data）进行有效的建模，另一方面得益于其非负的分解结构，可以用于替代传统的非负矩阵分解模型（NMF），因而被广泛应用于推荐系统、因子分析和聚类分析中。常见的贝叶斯泊松矩阵分解模型如下，其中观测值$x_{ij}$服从泊松分布，而其分解得到的因子矩阵的值则服从共轭的Gamma分布：

变分贝叶斯推断

问题描述

假设当前有一个贝叶斯模型，且其中的参数都有相应的先验分布。同时，模型中还可能有潜变量，将其与各种参数标记为$\Theta$。同样地，把所有观测变量集合标记为$\mathcal{Y}$。因此，我们希望找到分布$q(\Theta)$来逼近真实后验分布$p(\Theta\mid\mathcal{Y})$，而这可以通过最小化KL散度实现，也即：

其中$\text{ln}p(\mathcal{Y})$表示模型证据（Evidence），则其下界（lower bound）可以定义为$\mathcal{L}(q)=\int q(\Theta)\text{ln}{\frac{p(\mathcal{Y},\Theta)}{q(\Theta)}}d\Theta$。因为模型证据是一个常量，当KL散度为0时，下界出现最大值，这就意味着$q(\Theta)=p(\mathcal{Y},\Theta)$。